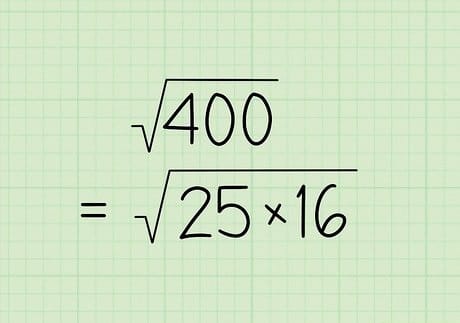شارح الدرس:
يعتبر درس تقدير الجذور التربيعية واحدا من أهم دروس منهج الرياضيات بالمملكة العربية السعودية للصف الثاني المتوسط الفصل الدراسي الأول.
ما هو الجذر التربيعي؟
يمكنك الآن معرفة تقدير الجذور التربيعية ومعرفة الجذر التربيعي وذلك من خلال موقع حلول كتبي وذلك من خلال السطور التالية:
- فإذا كان لدينا العدد (y)، فإن جذره التربيعي هو ذلك العدد الحقيقي الموجب (x).
- فإذا قمنا بضرب ذلك العدد (x) في نفسه تكون النتيجة هي العدد (y)، حيث يعتبر العدد (y) هو مربع العدد (x).
- علاوة على ذلك أنه قد تكون قيمة الجذر صحيحة كاملة، وقد تكون أيضًا قيمة الجذر قيمة عشرية.
- مثال على ذلك، يعتبر الرقم تسعة هو عبارة عن حاصل ضرب العدد 3 في نفسه مرة واحدة، أما بالنسبة للرقم 8 فهو عبارة عن حاصل ضرب العدد 83 في نفسه.
- الجدير بالذكر أنه توجد أكثر من طريقة لحساب الجذر التربيعي بسهولة ودون تعب.
- يمكنك أيضًا إيجاد الجذر التربيعي للأعداد المختلفة، حيث أنه قد تكون قيمة الجذر صحيحة كاملة، وقد تكون قيمة عشرية.
- يوجد طرق عديدة لحساب الجذر التربيعي، كما توجد الكثير من الخصائص التي تعمل على تسهيل تحديده.
طرق حساب الجذر التربيعي للأعداد
يمكنك القيام بعملية تقدير الجذور التربيعية، وإيجاد الجذر التربيعي وذلك عن طريق تطبيق المعادلة التالية:
- ق(س) = (س)^(1/2)
- حيث أن ق(س) هي اقتران قيمة ق بالقيمة س.
- (س)^(1/2) وهي القيمة س تحت الجذر التربيعي.
طريقة التخمين
- تعتبر هذه الطريقة هي إحدى الطرق التي يتم استخدامها لإيجاد الجذر التربيعي لعدد ما، وذلك عن طريق اقتراح عدة أرقام تساعد على الوصول إلى النتيجة الدقيقة.
- الجدير بالذكر أنه يوجد الكثير من الأمور التي تسهل من هذه الطريق، مثل:
- أنه لا يمكن أن يكون المربع الكامل عددا سالبًا.
- إذا انتهى العدد بالأرقام الآتية لا يوجد حينها جذر تربيعي كامل له، بل يوجد يكون الجذر التربيعي عدد عشري، وهذه الأرقام هي 2 أو 3 أو 7
- الأعداد التي تنتهي بالأرقام الآتية 1 أو 4 أو 5 أو 6 أو 9 يوجد لها جذر تربيعي تستطيع الوصول إليه بعدة احتمالات وبالتخمين.
التحليل للعوامل الأولية
- تعتبر طريقة التحليل باستخدام الأعداد الأولية هي واحدة من أهم طرق تقدير الجذور التربيعية.
- تعتمد طريقة تحليل العوامل الأولية على التفصيل والدقة بطريقة، حيث تقوم على إعادة وتحليل العدد نفسه إلى عوامله الأولية.
- الجدير بالذكر أنه عند ضرب العوامل الأولية بعضها البعض يؤدي ناتج ضربها إلى ذلك العدد الأصلي.
- ستلاحظ أنه عند النظر في العوامل الأولية الموجودة بعد قيامك بعملية التحليل أن كل اثنان منهما يشكل رقم، وأن ناتج ضربها هو الجذر التربيعي.
القسمة المطولة
- يمكن إيجاد الجذر التربيعي للأعداد التي تريدها باستخدام طريقة القسمة المطولة.
- عليك القيام بتقسيم العدد الذي تريد معرفة جذره التربيعي من اليمين إلى أزواج، بحيث يكون كل زوج وحده.
- عندما يتبقى رقم واحد يكن حينها ذو قيمة واحدة، بعد ذلك عليك القيام بدء إيجاد رقمين يمكن أن تقوم بضربهما معا.
- عند استخدام هذه الطريقة يكون الرقم المعطى أمامك أو الأقل منه أو الأكثر من، وذلك للقيام بتحديد الأعداد التي يقع بينها الجذر.
- لا تنسى أن تقوم بهذه الطريقة من اليسار لليمين.
- فمثلا لإيجاد الجذر التربيعي للعدد 784 بالقسمة المطولة، قم بتقسيم ذلك العدد إلى أزواج مثل (84) هو الزوج على أن يكون الرقم 7 وحده.
- بالنسبة للرقم 7، يمكنك اختيار (2 * 2 = 4) فيكون الناتج حينها أقل من 7، (3 * 3 = 9) يكون الناتج في هذه الحالة أكثر من سبعة، إذن نقوم باختيار العدد
- بعد ذلك نقوم بطرح 7 من 4 فيكون الناتج حينها هو 3، عن طريق إنزال العدد 84، يصبح كامل العدد
- ستلاحظ الآن أن العدد الذي يمكنك ضربه بنفسه لإعطاء الرقم 384 هو
- بعد ذلك قم باتخاذ الخانة الأولى لكل عدد من الأعداد السابقة، وذلك حتى تتحقق من هذه العملية، اضرب بنفسه لإعطاء الرقم الصحيح.
- بالنسبة للعدد 2 نأخذ 2، وبالنسبة للعدد 48 نأخذ 8، عند قيامك بترتيب الأعداد من اليسار لليمين، يكون العدد 28 هو الجذر التربيعي للعدد
- يمكنك الآن الحصول على حل جميع المسائل التي تتعلق بذلك الدرس، وذلك من خلال القيام بالضغط هنــــا.
إقرأ أيضًا: شرح وحل أسئلة درس التصحر واثره في البيئه
خواص الجذور التربيعية
يوجد خواص عديدة للجذور التربيعية خصائص عدّة، مثل:
- إذا انتهى العدد بالأرقام 1 أو 4 أو 5 أو 6 أو 9 فإن هناك جذر تربيعي ويمكن الوصول إليه عن طريق طرق عديدة مثل التجربة والتخمين.
- إذا كان الرقم عددًا مربعا كاملا فيكون له حينها جذر تربيعي كامل.
- تعطي الأعداد السالبة عند ضربها مع بعضها نتيجة موجبة.
- لا يوجد مربع كامل سالب.
- عند ضرب جذر الرقم بنفسه تكن النتيجة العدد نفسه.
- عند انتهاء الرقم بعدد زوجي من الأصفار، فيوجد حينها جذر تربيعي له.
- إذا انتهى العدد بالأرقام 2 أو 3 أو 7 أو 8 فإن لا يوجد جذر تربيعي كامل.
- عند ضرب رقمين تحت الجذر التربيعي، تكون النتيجة هي حاصل ضربهما تحت الجذر التربيعي أولا.
- المربع الكامل لا يمكن أن يكن سالبا نهائيا.
- عند ضرب الرقم تحت الجذر التربيعي بنفسه تحت الجذر التربيعي، تكون النتيجة حينها هي الرقم نفسه ولكن بدون الجذر.